In the simple case of a plane parallel plate, a ray of light which penetrates this plate is not diverted from its original direction. In a prism with faces set at angles to one-another, on the other hand, the ray undergoes a change of direction whose amount is dependent on several factors, viz.:
-
the wavelength of the light,
-
the form of the prism,
-
the refractive index of the prism material.
For dispersive brilliance the influence of the wavelength of the light is of particular importance. White light consists, as already stated, of a mixture of the basic colors contained in the spectrum: red, orange, yellow, green, blue and violet. Each of these colors spans a certain spread of wavelengths. They are:
| red | 780-640 nm |
| orange | 640-595 nm |
| yellow | 595-570 nm |
| green | 570-500 nm |
| blue | 500-400 nm |
| violet | 450-380 nm |
nm means nanometer. 1 nm = 0.000001 (one millionth) of 1 mm[(millimeter).
The shorter the wavelength of the rays, the more strongly the various color components are refracted. Red as the color of the longest wavelength has the smallest refractive index, Violet is diverted the most. The passage of a ray of white light through the sloping faces of a prism results in its splitting up into the spectral colors which are comprised in white light (Fig 188).

The numerical difference between the most widely divergent refractive indices for red and violet light is described as dispersion (0). Since both colors correspond to certain wavelength bands, the refractive indices are related to the so-called Fraunhofer lines B (in the red) and G (in the violet). These are unchanging dark lines in the spectrum of the sun, which the physicist FRAUNHOFER first observed and described by letters in alphabetical order. Since the refractive indices are:
n (violet) = 2.451 (corresponding to 430.8 nm of the G
line)
n (red) = 2.407 (corresponding to 687.0 nm of the B
line)
the dispersion in diamond is:
D = n (violet) - n (red) = 2.451 - 2.407 = 0.044.
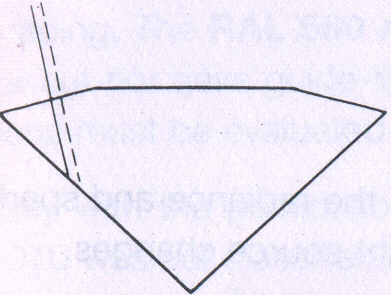
The degree of fanning out of the white light is primarily dependent on the angle of incidence of the light upon the surface when passing out into the air. When the incidence is directly within the critical angle of total reflection, the dispersion is at its greatest. For the brilliant cut this implies that the rays of light travelling from the interior of the brilliant to the crown facets should meet the upper facets at as great an angle as possible to the normal, so that a visible fanning out may be achieved. The angle of incidence must, however be less than 24°26', so that the rays are refracted into the air and not totally reflected. The following table and three sketches (Fig 189) demonstrate the dependence of the dispersion on the angle of incidence of the light.
 |
 |
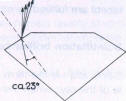 |
| Fig 189 Dispersion is dependent on the angle of incidence of light | ||
 |
 |
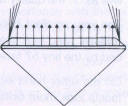 |
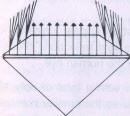
| Dispersion is dependent on the size of the crown facets | ||
| Angle of incidence to the normal | Angle of dispersion |
| 0° | 0° |
| 5° | 0°19' |
| 10° | 0°42' |
| 15° | 1°12' |
| 20° | 2°13' |
| 23°56' | 12°57' |
| over 24°26' | Total reflection |
Finally, the proportion of light which is totally reflected-in the stone's interior and then disperses. also depends on the size Of the crown facets in relation to that of the table of the brilliant. The smaller the table, the more light will be dispersed on the sloping crown facets (Fig 190 a). In brilliants with shallow crown and large table the major part of the light reflected on the pavilion facets passes through the table at right angles, without being scattered (Fig 190 b and c). At this Point old-cut brilliants may be recalled; though they sparkle with maximum "fire" through a high crown with small table and steep crown facets, their light emission remains poor because of the too-small table.
In the modern brilliant cut the requirements for maximum light emission through the table and for the greatest possible dispersion on the upper crown facets are fulfilled by an ideal blending 'of the proportions.
| Internal brilliance | Scintillation brilliance |